DEUG MIAS 2ième année
MIO2-2
Option Informatique Approfondie
Projet Réécriture
1998-99
Pascal Manoury
§ I -- Rappels : pointeurs, liste, arbres
1. Les listes
(1.a) Considérations abstraites
Les listes sont des structures de données permettant un
stockage et un traitement séquentiel des données. Abstraitement,
on peut définir les listes de façon récursives selon deux
clauses :
- soit la liste ne contient aucun élément, on dit alors
qu'elle est vide, on notera Nil;
- soit la liste commence par un élément x et se poursuit par
la liste xs, on notera Cons(x,xs).
Les symboles Nil et Cons sont appelés constructeurs des
listes. Toute liste est construites en utilisant ces
constructeurs. Par exemple, la liste contenant les entiers 1, 2 et 3
est obtenue en écrivant Cons(1,Cons(2,Cons(3,Nil))).
On n'accéde ``directement'' qu'au premier élément d'une liste et
quàu reste de la liste, lorsque celle-ci n'est pas vide. Pour
effectuer ces opérations, on se donne les opérateurs hd et tl
que l'on définit par les équations :
| hd(Cons(x,xs)) |
= |
x |
| tl(Cons(x,xs)) |
= |
xs
|
Le comportement de hd et tl n'est pas spécifiépour la liste
vide Nil : ces opérateurs sont partiels. Ces opérateurs sont
appelés accesseurs ou destructeurs des listes.
Remarque : on a, pour toute liste xs non vide
xs = Cons(hd(xs), tl(xs))
A partir de ces seules primitives, on peut définir TOUTES les
fonctions (calculables) sur les listes.
Exemple (1) : Calcul de la taille d'une liste : fonction size définie par
récurence sur son argument
| size(Nil) |
= |
0 |
| size(Cons(x,xs) |
= |
1+size(xs)
|
Supposons que nous disposions en PASCAL d'un type D donnéet
d'un type DList pour les listes d'éléments de type D ; des
constructeurs Nil et Cons ; des destructeurs hd et
tl. On peut définir la fonction size, en PASCAL
Function size(xs:DList) : Integer;
Begin
If xs = Nil then size := 0
Else size := 1 + size(tl(xs));
End;
(1.b) Considération plus concrètes
On veut pouvoir, àloisir, ajouter, retrancher des éléments
d'une liste, voire mettre deux listes bout àbout. Le nombre
d'éléments contenus dans une liste (que l'on appelle sa taille) peut donc varier de façon arbitraire et l'on ne veut pas
a priori fixer de limite maximum (la limite minimum est toujours
0) Pour réaliser cela, on a recours au mécanisme d'allocation
dynamique de mémoire mettant en oeuvre, en PASCAL, le
mécanisme des pointeurs.
Les pointeurs (rappels)
Un pointeur n'est rien d'autre qu'une réérence àun endroit de
la mémoire de la machine appelée adresse mémoire. En
PASCAL, toutes les données manipulées ont un type. En PASCAL donc,
tout pointeur est toujours un pointeur vers un objet d'un certain type.
On n'apas de pointeur en général, mais toujours un pointeur vers
donnée d'un type donné. Soit D un type de données, pour
déclarer le type DPtr des pointeurs vers une donnée de
type D, on utilise la syntaxe
Type
DPtr = ^D;
Le type D peut être aussi complexe que l'on veut : un entier,
un tableau, un enregistrement, un autre pointeur, etc ...
On déclare les variables de type pointeur selon la syntaxe usuelle
Var
p : DPtr;
On accède àla valeur pointée par p par la syntaxe
p^ L'expression p^ est de type D, lorsque DPtr
est définie comme D^. On a alors droit sur p^ àpresque1
toutes les opérations autorisées sur les variables de type D
- si D est le type Integer, on peut écrire
p^+0 ou p^:=0
- si D est un type tableau, on peut écrire
p^[2]
- si D est un type enregistrement dont l'un des champs est
c, on peut écrire
p^.c
Exemple (2) : Petit exemple de pointeur(s) sur un entier
Program exm1;
Type
intPtr = ^Integer;
Var
i : Integer;
p : intPtr;
q : intPtr;
Begin
i := 5;
writeln("i = ", i);
new(p);
p^ := i;
writeln("p^ = ", p^);
p^ := i+1;
writeln("i = ", i, " p^ = ", p^);
q := p;
writeln("q^ = ", q^, " p^ = ", p^);
p^ := p^+1;
writeln("q^ = ", q^, " p^ = ", p^);
End.
Listes chaînées (rappels)
Pour représenter les listes, nous utiliserons des enregistrements
comprenant deux champs : un champs contenant un pointeur sur un
élément de liste, un champs reliant cet élément au reste de la
liste. Une liste est un pointeur sur un tel enregistrement. Nous
supposons que les élément de la liste sont d'un certain type D.
Type
DPtr = ^D;
DList = ^DItem;
DItem =
Record
head : DPtr;
tail : DList;
End;
Définit alors les constructeurs et destructeurs des listes. Les cas
de la liste vide est simple : les listes étant des pointeurs, on
utilise le pointeur nul Nil. Les autres opérateurs sont
définis par :
Function Cons(x:D, xs:DList) : DList;
Var aux : DList;
Begin
new(aux);
new(aux^.head);
aux^.head^ := x;
aux^.tail := xs;
Cons := aux;
End;
Function hd(xs:DList) : D;
Begin
hd := xs^.head^;
End;
Function tl(xs:DList) : DList;
Begin
tl := xs^.tail;
End;
Exercice (1) : Ecrire une fonction last qui retourne la valeur (de type
D) du dernier élément d'une liste non vide.
Remarque (1) : Il n'est pas toujours possible d'obtenir une
fonction hd retournant un objet de type D En effet, en
PASCAL, le type de retour d'une fonction doit être simple : un
entier, un réel, un pointeur, etc... Si l'on veut donc constituer
des listes d'objets plus complexes, la fonction hd ne pourra
retourner qu'un pointeur sur une structure représentant l'objet.
Exercice (2) : Listes d'association avec ses primitives assoc, memassoc, addassoc (sans duplication de clé)
(1.c) Listes chaînées (discussion)
Une opération courante sur les liste est l'opération de concaténations que nous noterons append. Selon notre habitude,
nous la définissons par le système d'équations récursives :
| append(nil, ys) |
= |
ys |
| append(Cons(x,xs), ys) |
= |
Cons(x, append(xs,ys))
|
En utilisant les primitives définies en [X], nous
définissons la fonction append comme
Function append(xs:DList, ys:DList) : DList;
Begin
If xs = Nil then append := ys
Else append := Cons(hd(xs), append(tl(xs), ys))
End;
Soient l, l1 et l2 trois listes. Aprés exécution
de l'instruction
l := append(l1, l2);
on obtient un résultat illustrépar la figure suivante :
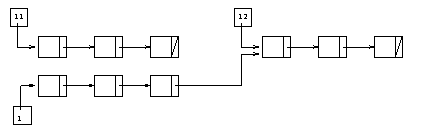
où la liste l1 a étédupliquée.
Ce résultat n'est pas toujours souhaitable : il consomme inutilement
de la mémoire si l'on ne veut plus se servir de la liste originelle
l1. Dans ce cas, on aimerait plutôt obtenir :
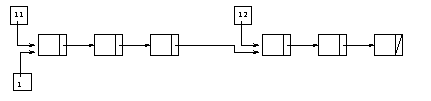
Pour obtenir ce second résultat, il faut pouvoir modifier la
valeur du champs tail de la dernière cellule de l1 en
lui donnant la valeur l2 et l peut alors recevoir la
valeur l1.
Considérons maintenant le problème suivant : obtenir une liste
xs' àpartir d'une liste xs dont on modifie la valeur du premier
élément. En n'utilisant que nos primitives actuelles, nous
écrivons une fonction modifHead :
Function modifHead(xs:DList, x:D) : DList;
Begin
modifHead := Cons(x, tl(xs));
End;
Ici encore, nous avons créé(par l'appel àCons)
une2
nouvelle cellule contenant x alors que l'on aurait peut être
simplement voulu modifier en place la valeur du premier
élément.
Pour tenir compte de ces remarques, il nous faut sortir du cadre
purement fonctionnel qui a étéla notre jusqu'àprésent pour
introduire des opérations avec effet de bord sur les objets
manipulés.
Soient donc les procédures setHead et setTail qui
modifient, respectivement, la valeur de l'élément contenu en
tête et la valeur de la suite de la liste passée en premier argument.
Procedure setHead(xs:DList, x:D);
Begin
hd(xs)^ := x;
End;
Procedure setTail(xs:DList, ys:DList);
Begin
tl(xs) := ys;
End;
La procédure setHead fait exactement la modification en place
de la valeur du premier élément de la liste. Pour obtenir une
fonction de concaténation procédant par effet de bord, nous nous
donnons une fonction auxiliaire lastTail retournant la
dernière cellule, de type DLIst d'une
liste3
ou nil si la
liste est vide.
Function lastTail(xs:DList) : DList;
Begin
If xs = nil then lastTail := nil
Else If tl(xs) = nil then lastTail := xs
Else lastTail := lastTail(tl(xs))
End;
On définit alors une nouvelle fonction de concaténation DListCat4
comme :
Procedure DListCat(xs:DList, ys:DList);
Begin
setTail(lastTail(xs), ys);
End;
Commentaire (1) : Nous avons choisi àdessein d'implanter setHead, setTail
et DLIstCat comme des Procedure et non des Function. Une procédure ne retourne pas de valeur. Si elle a un
effet, c'est un effet de bord. C'est pour souligner cette
propriétéde setHead, setTail et DLIstCat que
nous utilisons une définition comme Procedure.
Exercice (3) : Soit f une fonction de signature Function f(x:D) : D,
écrire une procédure qui remplace tous les éléments x
d'une liste xs par le résultat de f(x).
Soit p une procedure de signature Procedure p(x:D),
écrire une procédure qui applique àtous les éléments x d'une liste xs la procédure p.
Exercice (4) : On pose Type D = Integer;.
Ecrire une procédure d'affichage des listes d'entiers.
On souhaite, par exemple, que la liste obtenue
par Cons(1, Cons(2, Cons(3, Nil))) soit affichée sous la forme
[1;2;3] et que la liste vide soit affichée sous la forme [].
Ecrire une fonction intListOfString de signature
Function intListOfString(s:String) : DList qui analyse une
chaîne de caractère sensée contenir une liste au format
ci-dessus et renvoie la liste (de type DList) correspondante.
Exercice (5) : Proposez un amendement de la structure de listes de façon àce que la fonction lastTail soit immédiate.
2. Les arbres
Les arbres, comme les listes, peuvent être vues comme des structures
récursives des stockages de données. Il y a quelques variantes sur
l'endroit oùles données sont rangées dans la structure : àchaque niveau de l'arbre; seulement au plus bas niveau; ou
partout. L'autre variante possible est le nombre d'embranchements :
arbres binaires; arbres ternaires voire arbres dits planaires
généraux. C'est cette dernière variante que nous utiliserons.
Nous nous permettrons d'utiliser le simple terme d'arbre pour
désigner de telles structures.
(2.d) Considérations abstraites
Comme nous l'avons fait pour les listes, définissons abstraitement
l'ensemble de arbres planaires généraux, dits aussi arbres àembranchements finis, en termes de constructeurs :
- un arbre peut être vide, on notera Empty ;
- pour tout entier n, si t1, .., tn sont des arbres et x
un élément alors on peut construire l'arbre de racine x
dont les sous-arbres sont t1, .., tn, on notera Brn(x, t1, ..,
tn).
La constante Empty et l'infinitéd'opérateurs Brn sont les
constructeurs des arbres.
Voici un exemple de représentation graphique d'un arbre
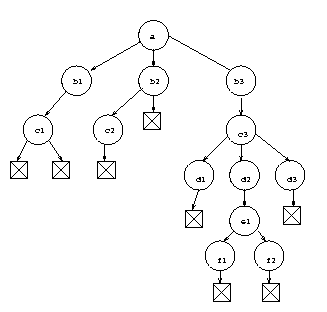
Son écriture linéaire correspondante est :
|
Br3(a, |
Br1(b1,Br2(c1,Empty,Empty)), |
| |
Br2(b2, Br1(c2, Empty), Empty), |
| |
Br1(b3, Br3(c3, |
Br1(d1, Empty), |
| |
|
Br1(d2, Br2(e1, Br1(f1, Empty), Br1(f2, Empty))), |
| |
|
Br1(d3, Empty))))
|
Comme l'illustre notre exemple, une telle définition des arbres
multiplie de façon incontrolable l'utilisation de l'arbre vide pour
``terminer'' la structure. Nous choisirons une définition
alternative dans laquelle nous remplaçons le constructeur Empty
par un constructeur Leaf : une feuille contenant uniquement un
élément de donnée. Ce qui conduit àla définition suivante.
- si x est un élément alors Leaf(x) est un arbre.
- pour tout entier n, si t1, .., tn sont des arbres et x
un élément alors Brn(x, t1, .., tn) est un arbre.
Notre exemple se dessine alors
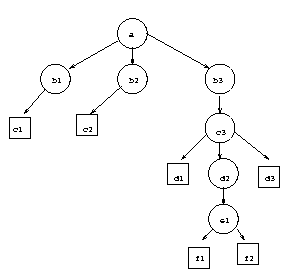
et s'écrit
|
Br3(a, |
Br1(b1,Leaf(c1)), |
| |
Br1(b2, Leaf(c2), |
| |
Br1(b3, Br3(c3, |
Leaf(d1), |
| |
|
Br1(d2, Br2(e1, Leaf(f1), Leaf(f2))), |
| |
|
Leaf(d3))))
|
Nous avons perdu la possibilitéd'avoir un arbre vide, mais
certaines application, dont celle que nous avons en tête, s'en
passent trés bien !
(2.e) Un codage avec les listes
Plutôt que de considérer une famille de constructeurs Brn oùn est un entier, on peut ne considérer qu'un seul constructeur
binaire dont le second argument est la liste des sous-arbres. On
obtient alors la définition :
- si x est un élément alors Leaf(s) est un arbre.
- si x est un élément et ts une liste d'arbres alors
Br(x,ts) est un arbre.
Notons que nous réintroduisons subreptissement la possibilitéde
construire de fausses feuilles en utilisant une liste vide
de sous arbres : Br(x,Nil).
Les sous-arbres de la définition récursives sont ici encapsulés
dans la structure de liste ts. On n'y a pas accés directement,
mais en déstructurant la liste. On aura donc sur les arbres
planaires ainsi définit un style de programmation particulier.
Par exemple, on définira une fonction de transformation d'un arbre
en liste5
àl'aide deux deux fonctions mutuellement récursives : listOfTree et listOfTrees.
| listOfTree(Leaf(x)) |
= |
Cons(x, Nil) |
| listOfTree(Br(x,ts)) |
= |
Cons(x, listOfTrees(ts)) |
| |
|
|
| listOfTrees(Nil) |
= |
Nil |
| listOfTrees(Cons(t,ts)) |
= |
append(listOfTree(t), listOfTrees(ts))
|
(2.f) Implantation
Pour implanter notre structure d'arbre, nous devons définir àla fois les arbres et les listes d'arbres. De plus, nous devons
distinguer parmi les arbres ceux qui sont de simples feuilles de ceux
qui sont des branchements.
Le premier point ne pose pas de difficultépuisque les listes sont
des pointeurs et peuvent être déclarées avant la
définiton de l'objet sur lequel elles pointent. Pour réaliser le
second point, il faut pouvoir définir un type dit type
union. Le langage PASCAL propose pour cela une catégorie
particulière d'enregistrements dits variables oúun champs,
pris dans un type énuméré, sert de marqueur entre les
différentes sortes de données.
Type
TList = ^TItem;
TPtr = ^DTree;
TItem =
Record
head : TPtr;
tail : TList;
End;
TSort = (leafT, brT);
DTree =
Record
elt : DPtr;
Case tag:TSort of
brT : (subTrees : TList);
End;
Exercice (6) : Implanter le constructeur ConsTList, les destructeurs hdTList et tl TList ainsi que la fonction de concaténation
TListCat pour les listes d'arbres (remarquons que l'on peut
conserver la constante Nil pour la liste d'arbre vide)
Exercice (7) : Définir les constructeurs Leaf et Br des
arbres. Définir les destructeurs eltOf et subTreesOf
ainsi que deux fonctions de reconnaissance : isLeaf et isBr.
Muni de ces functions de base, on peut implanter les fonction
mutuellement listOfTree et listOfTrees en utilisant la
directive forward permettant de déclarer une fonction avant de
la définir effectivement.
Function listOfTrees(ts : TList) : Dlist ; Forward ;
Function listOfTree(t : DTree) : DList ;
Begin
If isLeaf(t) then listOfTree := Cons(eltOf(t), Nil)
Else listOfTree := Cons(eltOf(t), listOfTrees(subtreesOf(t)))
End;
Function listOfTrees(ts : TList) : DList;
Begin
If (ts=Nil) then listOfTrees := Nil
Else listOfTrees := appendTList(listOfTree(hdTList(ts)),
listOfTrees(tlTList(ts)))
End;
Exercice (8) : Ecrire une procédure d'affichage des arbres sous forme
linéaire (on affichera les listes comme en dans l'exercice
X)
§ II -- Les termes : définition, implantation
3. Définition
Les mathématiques, aussi bien que l'informatique vous ont habitués
àmanipuler des termes que l'on appelle plus volontier expressions en informatique. Par exemple, 1+(3× 4),
1+(2× x), f(x)+1 sont des termes. On reconnait dans les
termes trois catégories de symboles : les constantes (1, 2,
etc..) les variables (x, etc..) et les fonctions (+, ×,
f, etc..) On peut uniformiser la notation des termes qui mélange
ici notation infixe et notation préfixe des fonctions en ne
décrétant valide que la seule notation préfixe. Ce que l'on
écrit usuellement 1+(f(x)× 2) devient alors : +(1,
×(f(x),2)).
De façon générale, on définit un ensemble
de termes par la donnée de trois ensembles de symboles et de deux
(ou trois) règles de construction des termes. On ne se soucis pas
encore d'interpréter les symboles (ie : on utilise le
symbole + sans soucis de savoir qu'il représente l'addition). En
d'autre termes : on définit une syntaxe sans en donner la sémantique.
Soient donc
- C un ensemble fini ou dénombrable de symboles de constantes,
- X un ensemble dénombrable de symboles variables,
- F un ensemble fini ou dénombrable de symboles de fonctions.
On demande que ces trois ensembles soient deux àdeux disjoints.
Chaque fonction mathématique (ou informatique) réclame un nombre
donnéd'arguments : l'addition a besoin de deux arguments, la
fonction logarithme n'en a besoin que d'un. On dit que l'addition est
binaire alors que la fonction logarithme est unaire. On
dit aussi que l'addition est d'arité 2 alors que la fonction
logarithme est d'arité1. Pour écrire correctement un terme, il
faut connaître l'aritédes symboles de fonction. On munit donc
l'ensemble F d'une fonction d'aritéa : F®IN
Si fÎF et a(f)=n, pour nÎIN, nous dirons que f
est d'aritén ou que f est n-aire (prononcer :
``ènaire'')
Nous pouvons àprésent définir récursivement l'ensemble
T des termes par :
- CÌT (tout symbole de constante est un terme) ;
- XÌT (tout symbole de variable est un terme) ;
- pour tout t1Î T, .., tnÎ T, pour tout fÎF si
a(f)=n alors f(t1, .., tn)Î T (si f est un symbole de
fonction d'aritén et t1, .., tn sont des termes, alors
l'application de f aux n arguments t1, .., tn est un terme).
On a que tout terme t est soit une variable xÎ X, soit une
constante cÎ C, soit de la forme f(t1, .., tn) avec fÎ F
et t1, .., tn des termes. On utilisera ces différents cas de
construction des termes pour définir (récursivement, dans la
plupart des cas) propriétés ou fonctions sur les termes. Par
exemple on définit l'ensemble des variables apparaissant dans un
terme t, que l'on note V(t), par :
- si t est une constante alors V(t)=Ø
- si t est la variable x alors V(t)={x}
- si t est de la forme f(t1, .., tn) alors V(t) =
Èi=1nV(ti)
Un notion utile sur les termes est celle de sous
terme. Intuitivement, un terme t' est un sous terme de t si t'
<< apparaît >> dans t. Plus formellement, on définit,
récursivement sur t, l'ensemble ST(t) des sous termes de t
- Si t est une variable ou une constante alors ST(t)={t}.
- Si t est de la forme f(t1, .., tn) alors
ST(t) = {t}ÈÈi=1nST(ti)
On dit que v est un sous terme de t si et seulement si vÎ ST(t).
4. Implantation
L'écriture des termes telle que nous venons de la définir rappelle
ce que nous avions appelénotation linéaires des arbres. On
peut donc, àl'inverse, représenter graphiquement les termes par
des structures arborescentes. Ainsi, le terme +(1,*(f(x),2))
peut être dessinécomme l'arbre :

Notre implantation de la structure des termes sera donc fortement
inspirée de celle des arbres. Chaque noeud sera étiquetépar
un nom de symbole. Dans le cas oùce symbole est un symbole de
fonction, nous aurons autant de sous arbres que l'indique l'aritédu
symbole.
Type
TList = ^TItem;
Term = ^TData;
TItem =
Record
head : Term;
tail : TList;
End;
TSym = (varSym, cstSym, funSym);
TData =
Record
name : String;
Case tag:TSym of
funSym : (args : TList);
End;
On se donne, sur les termes (et les listes de termes) les
primitives suivantes :
Termes : constructeurs
Function TCst(c : String) : Term;
Function TVar(x : String) : Term;
Function TFun(f : String; ts : TList) : Term;
Termes : accesseurs
Function nameOf(t : Term) : String;
Function symOf(t : Term) : TSym;
Function argsOf(t : Term) : TList;
Modificateur physique
Procedure setTerm(Var t : Term; u : Term);
Listes de termes : constructeur
Function ConsTList(t:Term; ts:TList) : TList;
La liste vide reste le pointeur nul : Nil
Listes de termes : accesseurs
Function hdTList(ts:TList) : Term;
Function tlTList(ts:TList) : TList;
Exercice (9) : Définir une fonction d'affichage des termes (cf affichage
des arbres).
Exercice (10) : Définir une fonction booléenne qui prend en argument deux
termes t et v et retourne true si et seulement si
v est un sous terme de t.
5. De l'égalitéentre termes
Considérons les deux termes suivants : 2+2 et 2*2. Nul ne
s'étonnera que l'on écrive 2+2=2*2. Cependant, ces deux termes ne sont pas égaux ! L'arbre représentant 2+2 et l'arbre
représentant 2*2 ne sont pas la même structure. A
l'inverse, le même terme peut désigner deux objets différents :
par exemple, on peut avoir que 1+1=2 si l'on utilise le symbole +
pour dénoter l'addition sur les entiers, mais on peut avoir
également que 1+1=1 si l'on utilise le symbole + pour dénoter
la disjonction booléenne.
Il nous faut donc distinguer deux catégories d'égalité:
l'égalitéusuelle que l'on manipule lorsque l'on a assignéune
interprétation aux symboles de fonctions (et de constantes) ;
l'égalitéstructurelle qui ne considère que l'identitéd'écriture ou de représentation des termes.
Exercice (11) : définir une fonction booléenne eqT qui teste
l'égalitéstructurelle entre deux termes.
Au niveau du langage PASCAL, on retrouve également cette dichotomie
entre l'égalitédu langage dénotée par le symbole = et
l'égalitéstructurelle définie par la fonction eqT. Dans
le cas de notre structure Term, si le résultat de t=u est
True, nous dirons que t et u sont physiquement
égaux : leurs représentations partagent exactement le même
espace mémoire.
Duplication
Nous aurons besoin par la suite de dupliquer un terme ou un sous terme
donné. C'est àdire, créer une copie u d'un terme
donnét telle que eqT(t,u)=True, mais t et
u sont physiquement différents (au quel cas : t=u=False) On définit pour cela une fonction de clonage : cloneT
Function itCloneT(ts : TList) : TList; Forward;
Function cloneT(t : Term) : Term;
Begin
Case symOf(t) of
varSym : cloneT := TVar(nameOf(t));
cstSym : cloneT := TCst(nameOf(t));
funSym : cloneT := TFun(nameOf(t), itCloneT(argsOf(t)));
End;
End;
Function itCloneT(ts : TList) : TList;
Begin
If ts=Nil then itCloneT := Nil
Else itCloneT := ConsTList(cloneT(hdTList(ts)), itCloneT(tlTList(ts)));
End;
Désallocation
Les clones que nous créerons seront, pour la plus part, des
structures temporaires. Pour ne pas encombrer inutilement la
mémoire, nous devrons libérer cet espace. On utilise pour cela la
primitive dispose de PASCAL.
Procedure itDisposeT(Var ts : TList); Forward;
Procedure disposeT(Var t : Term);
Var aux : TList;
Begin
If t<>Nil then
Begin
If symOf(t)=funSym then
Begin
aux := argsOf(t);
itDisposeT(aux);
End;
dispose(t);
t := Nil;
End;
End;
Procedure itDisposeT(Var ts : TList);
Var aux1 : TList;
Var aux2 : Term;
Begin
If ts<>Nil then
Begin
aux2 := hdTList(ts);
disposeT(aux2);
aux1 := tlTList(ts);
itDisposeT(aux1);
dispose(ts);
ts := Nil;
End;
End;
§ III -- Substitution
6. Définition
Formellement, une substitution est une application de l'ensemble
des variable X dans l'ensemble des termes T. Si s est une
substitution, on peut l'étendre en une application de l'ensembles
des termes dans l'ensemble des termes. Par abus de langage, on
continue d'appeler substitution s cette nouvelle
application. Intuitivement, si t est un terme, le terme sigma(t)
est le terme obtenu en remplaçant chaque variable x de t par le
terme s(x). Formellement, on définit récursivement
s(t) par :
- si t est une constante c, s(t)=c ;
- si t est une variable x, s(t)=s(x) ;
- si t est de la forme f(t1, .., tn),
s(t)=f(s(t1), .., s(tn))
Dans la pratique, les substitutions sont rarement définies sur
l'ensemble des variables dans son entier. On se contente de remplacer
un nombre fini (et souvent petit) de variables. Une substitution est
alors une liste (finie) d'association dont les clés sont les noms de
variables et les valeurs associées, des termes. On notera [u1/x1,
.., um/xm] les substitutions et t[u1/x1, .., um/xm] le terme
obtenu par application de la substitution. Ce terme est défini par :
- si t est une constante c, t[u1/x1, .., um/xm]=c ;
- si t est une variable x telle que xÏ{x1, ..,
xm}, t[u1/x1, .., um/xm]=x ;
- si t est une variable xiÎ{x1, ..,xm},
t[u1/x1, .., um/xm]=ui ;
- si t est de la forme f(t1, .., tn),
t[u1/x1, .., um/xm]=f(t1[u1/x1, .., um/xm], .., tn[u1/x1,
.., um/xm])
Remarquons que si nous voulons que les substitutions représentées
sous la forme [u1/x1, .., um/xm] restent des applications, il
faut supposer que les variables x1, .., xm sont deux àdeux
distinctes.
7. Implantation
Pour constituer les listes d'association qui représentent les
substitutions, nous commençons par définir le type des paires
(variable, terme) Nous ne retiendrons des variables que leur nom, et,
tenant compte de la remarque X, nous manipulerons les
paires via un pointeur. Ce qui donne :
Type
STPair = ^STItem;
STItem =
Record
key : String;
val : Term;
End;
Exercice (12) : nous laissons en exercice l'implantation du constructeur
Function newSTPair(x : String; t : Term) : STPair;
et des accesseurs :
Function keyOf(xt : STPair) : String;
Function valOf(xt : STPair) : Term;
Nous recommandons également l'écriture d'une fonction d'affichage
des paires sous la forme t/x
On définit alors le type LSubst comme liste d'association,
selon notre procéder habituel :
Type
LSubst = ^SItem;
SItem =
Record
head : STPair;
tail : LSubst;
End;
Exercice (13) : Comme d'hab'
Function ConsLSubst(xt:STPair; xts:LSubst) : LSubst;
Function hdLSubst(xts:LSubst) : STPair;
Function tlLSubst(xts:LSubst) : LSubst;
Procedure writeLSubst(xts : LSubst);
Avec, en plus
Procedure disposeLSubst(Var xts : LSubst);
Procedure setTlLSubst(xts : LSubst; yus : LSubst);
La fonction assocLSubst de recherche de valeeur associée àune clépeut échouer. Ce qu'il faut pouvoir signaler au code
appelant. Nous profiterons ici de ce que les valeurs associées sont
de pointeurs (cf type Term) pour utiliser le pointeur nul
comme constat d'échec. En notant (y,v) les paires, la
spécification équationnelle de la fonction assoc, en
général, est
| assoc(x,Nil) |
= |
Nil |
|
| assoc(x,Cons((y,v), yvs) |
= |
v |
, si y=x |
| assoc(x,Cons((y,v), yvs) |
= |
assoc(x, yvs) |
, sinon
|
Exercice (14) : Ecrire Function assocLSubst(x:String; xts:LSubst) : Term;
L'application d'une substitution àun terme est implantépar la
procédure
Procedure itSubst(ts:TList; xts:LSubst); Forward;
Procedure subst(t:Term; xts:LSubst);
Var aux : Term;
Begin
Case symOf(t) of
varSym : Begin
aux := assocLSubst(nameOf(t), xts);
If aux <> Nil then setTerm(t, cloneT(aux));
End;
funSym : itSubst(argsOf(t), xts)
End;
End;
Procedure itSubst(ts:TList; xts:LSubst);
Begin
If ts<>Nil then
Begin
subst(hdTList(ts), xts);
itSubst(tlTList(ts), xts);
End;
End;
Remarquons que dans le cas oùla substitution est effective (le
terme t est une variable), nous procédons (d'oùla
Procedure) àune modification en place du terme (procédure
setTerm) et, de plus, nous opérons la substitution avec un
clone du terme associé(aux) àla variable. L'utilisation du
clone permet d'éviter, si la variable a plusieurs occurences dans
t, le partage de la représentation d'un même sous terme : ce
partage n'est pas souhaitable pour l'application que nous avons en
vue.
8. Construction des substitutions
Enfin, pour la suite des événements, nous aurons besoin d'une
fonction addLSubst d'enrichissement des substitutions. Cette
fonction devra rajouter une nouvelle paire (y,v) àune liste yvs
si et seulement si ou bien (y,v) n'apparaît pas dans yvs. Dans
le cas oùyvs contiendrait une paire (y,w) avec w¹v, la
fonction devrait signaler une erreur que nous appellerons un clash.
Pour implanter cette fonction, nous nous donnons les impératifs :
faire une modification en place de la liste yvs
laisser inchangée la liste yvs en cas de redondance ((y,v) existe
déjà) ou de clash
Ces deux impératifs nous conduisent àimplanter une
Procedure plutôt qu'une fonction. Et comme nous ne pourrons
utiliser l'astuce du pointeur nul comme constat d'échec, cette
procédure aura comme argument un booléen siganlant l'occurrence
d'un clash ou non. On obtient
Procedure addLSubst(Var clash : boolean; Var xts : LSubst; xt : STPair);
Var aux1 : STPair;
Procedure addSubstRec(Var xts : LSubst);
Var aux2 : LSubst;
Begin
If xts=Nil then
xts := ConsLSubst(xt,Nil)
Else
Begin
aux1 := hdLSubst(xts);
If keyOf(aux1)=keyOf(xt) then
clash := not (eqT(valOf(aux1),valOf(xt)))
Else
Begin
aux2 := tlLSubst(xts);
addSubstRec(aux2);
setTlLSubst(xts, aux2);
End;
End;
End; { addSubstRec }
Begin { addLSubst }
clash := False;
addSubstRec(xts);
End; { addLSubst }
§ IV -- Filtrage
9. Définition
On appelle filtrage une relation entre termes mettant en
oeuvre les subtitutions. On dit qu'un terme t filtre un
terme u si et seulement si il existe une substitution s telle
que s(t)=u. Nous dirons, plus précisément que t filtre
u selon s.
Par exemple, si t est le terme n+0 et que u est le terme
(m+1)+0 (oùn et m sont des variables) alors, en prenant
s=[m+1/n] on obtient t[m+1/n]=u On peut dire que si t
filtre u alors u est un cas particulier de t : on obtient u en
remplaçant dans t certaines variables par des termes
particuliers. Un cas particulier de filtrage est celui oùles deux
termes sont déjàégaux : 0+1 filtre 0+1 selon la
substitution vide [].
Il faut prendre garde que les substitutions sont des fonctions : elles
ne peuvent associer des termes différents àune même
variable. Ainsi le terme n+n ne filtre pas 0+1, ni 0+m, ni m+p
(oùn, m et p sont les variables)
Le problème que nous aurons àtraiter est : étant donnés deux
termes t et u, est-ce que t filtre u, et, si oui, quelle est
la substitution qui égalise les deux termes ? Il nous faut pour cela
une définiton plus constructive de la relation de
filtrage. Cette nouvelle définition nous permettra de donner un
algorithme décidant de la question du filtrage entre deux termes.
Selon l'habitude maintenant bien établie, nous procéderons par
récurrence sur la structure des termes pour donner une première
redéfinition de la relation de filtrage.
- si t est la variable x alors t filtre u selon [u/x].
- si t est la constante c ainsi que u alors t filtre u
selon [].
- si t est de la forme f(t1, .., tn), si u est de la
forme f(u1, .., un) et si, pour tout iÎ[1..n], ti filtre
ui selon s alors t filtre u selon s.
- tout autre cas est un cas d'échec appeléclash.
Si cette définition permet de décider du cas trivial du filtrage
(lorsque t est une variable) elle reste encore trop générale
pour le cas oùt est de la forme f(t1, .., tn) : on ne sait
toujours pas comment construire s.
En examinant ce dernier cas, nous avons que si chaque ti filtre
chaque ui selon une substitution si, pour que t filtre u
il faut obtenir àpartir des si une seule substitution
s. Pour cela, il faut simplement que les si soient
cohérentes : qu'elles associent chacune un même terme aux
mêmes variables. Si tel est le cas, on fusionne toutes les
si en une seule substitution. On notera
s1Ås2 la fusion des substitions s1 et
s2.
Exercice (15) : écrire la fonction de fusion (indication : utiliser la
procédure addLSubst)
10. Algorithme
Sachant que l'on peut traiter localement les sous termes t1, ..,
tn, reste encore, pour obtenir une définition complètement
constructive, àéliminer les points de suspension (..) de
l'écriture des termes. Nous utilisons pour ce faire le remplacement
des n-uplets t1, .., tn par des structures de listes. Pour
construire la substitution s résultant de la fusion des
s1, .., sn, nous procédons pas àpas par induction
structurelle sur les listes de termes àcomparer.
On retrouve alors notre schèma de définitions mutuellement
récursives et on définit àla fois le filtrage entre termes et le
filtrage entre listes de termes :
- Filtrage entre termes :
- si t est la variable x alors t filtre u selon [u/x].
- si t est la constante c ainsi que u alors t filtre u
selon [].
- si t est de la forme f(ts), si u est de la forme f(us)
(oùts et us sont deux listes de termes) et si ts filtre us
selon s alors t filtre u selon sigma.
- sinon, on a un clash.
- Filtrage entre listes de termes :
- si ts et si us sont toutes deux la liste vide [] alors
ts filtre us selon la substitution vide [].
- si ts est de la forme Cons(t, ts'), si us est de la forme
Cons(u, us'), si le terme t filtre le terme u selon la
substitution s et si la liste ts' filtre la liste us' selon
la substitution s' alors ts filtre us selon
sÅs'.
- dans tout autre cas, on a un clash.
Exercice (16) : implanter l'algorithme ci-dessus par deux procédures :
Procedure match(t:Term; u:Term; Var s:LSubst; Var clash:Boolean);
Procedure itmatch(ts:TList; us:TList; Var s:LSubst; Var clash:Boolean);
La liste s contiendra, si elle existe, la substitution selon
laquelle t (resp. ts) filtre u (resp. us). Le
booléen clash indiquera s'il y a ou non un clash entre
les (listes de) termes.
11. Recherche de motif
Dans le cadre de la réécriture, nous utiliserons la relation de
filtrage de la fa con suivante : soit p un terme appelémotif (en anglais pattern) et soit t un terme, le problème
que nous cherchons àrésoudre est celui de savoir s'il existe un
sous terme t' de t tel que p filtre t.
L'algorithme de recherche d'un motif p dans un terme t est
simple. Il procède par induction mutuelle sur les termes et listes
de termes. Nous demanderons, qu'en cas de succé, il fournisse àla
fois la substitution et le sous terme filtré. En supposant que l'on
a une fonction match telle que match(p,t)=s si p filtre t
selon s et match(p,t)=clash sinon, on définit deux
fonctions tryMatch et itTryMatch par le système d'équations
| tryMatch(p,t) |
= |
(s, t) |
, si match(p,t)=s |
| tryMatch(p,f(ts)) |
= |
itTryMatch(p,ts) |
, si match(p,f(ts))=clash |
| |
|
|
|
| itTryMatch(p,[]) |
= |
clash |
|
| itTryMatch(p, Cons(t,ts') |
= |
(s, t) |
, si tryMatch(p,t)=s |
| itTryMatch(p, Cons(t,ts') |
= |
itTryMatch(p,ts) |
, sinon
|
Exercice (17) : Implanter l'algorithme de recherche de motif par deux
procédures :
Procedure tryMatch(p : Term; t:Term; Var s:LSubst; Var clash:boolean; Var v:Term);
Procedure itTryMatch(p : Term; ts:TList; Var s:LSubst; Var clash:boolean; Var v:Term);
Les résultats seront donnés dans les variables s et clash.
§ V -- Règles de réécriture
Nous abordons maintenant l'ultime ligne droite avant la mise en
application des systèmes de réécriture. Nous allons voir dans ce
paragraphe ce qu'est une règle de réécriture, comment
plusieurs règles se combinent pour former un système de
réécriture et, enfin, comment appliquer ces règles pour
définir une relation de réécriture.
Une règle de réécriture un couple de termes (l,r)
que l'on note l® r. Une règle de réécriture est donc
orientée. Le terme l est le membre gauche de
la règle et r est son membre droit.
Intuitivement, pour appliquer une règle l® r àun terme
t, on cherche un sous terme t' de t tel que l filtre t'
selon, disons, s, puis on remplace le sous terme t' par celui
obtenu en appliquant s àr.
12. Définitions
Nous donnons dans ce paragraphe la définition formelle de la
relation de réécriture. Il nous faut, pour y parvenir, préciser
la notion intuitive de << remplacement >> d'un sous terme.
Considérons le terme f(g(a,h(x)), h(x)). Si nous nous contentons
de dire << nous remplaçons le sous terme h(x) par b >>
Pour proférons un énoncéambigu : lequel des deux h(x) faut-il
remplacer ? Pour lever cette ambiguïté, nous introduisons la
notion d'occurence qui a pour rôle de permettre de désigner
sans ambiguïtéun sous terme d'un terme.
Rappelons nous que les termes ont une structure
d'arbre. Intuitivement, on peut dénoter un sous arbre d'un arbre, en
indiquant le chemin que l'on parcours, en partant de la racine,
pour atteindre ce sous arbre. Pour noter les chemins, on utilise les
suites finies (possiblement vides) d'entiers strictement positifs. On
note la suite vide et, si x est une suite et i un
entier (strictement positif), on note i.x la suite commençant par
i et se poursuivant par x.
Dans le domaine de la réécriture (et des termes) on parle d'occurence plutôt que de chemin. On définit, par induction sur t
l'ensemble O(t) des occurences de t.
- O(t)=, si tÎC ou tÎX,
- O(t)={}È{i.o | iÎ[1..n] et
oÎO(ti)}, si t=f(t1, .., tn).
Si oÎO(t), on définit le sous terme de t d'occurrence
o, notét|o par les deux clauses :
- t|= t et
- f(t1, , ti, .., tn)|i.o = ti|o.
Si oÎO(t), on définit l'opération de remplacement d'un
terme u àl'occurrence o de t, notée t[o¬ u], par
les deux clauses :
- t[¬ u]=u et
- f(t1, , ti, .., tn)[i.o¬ u] = f(t1, ..,ti[o¬
u], .., tn).
Si l® r est une règle de réécriture, on dit qu'elle est
applicable àun terme t si et seulement si il existe
oÎO(t) telle que l filtre t|o selon s. Lorsqu'une
règle l® r est applicable àun terme t (àune
occurence o, selon une substitution s) le résultat de
l'application de cette règle àce terme est le terme
t' = t[o¬ s(r)] on dit que t se réécrit (par
l® r) en t', on note t® t'. En itérant le
processus de réécriture sur chaque nouveau résultat obtenu, on
obtient une chaîne de réécritures. Si le dernier terme
de cette chaîne est u, on note t ®* u.
Un ensemble de règles de réécriture forment un système de
réécriture. Si R est un système de réécriture, on dit
qu'un terme t se réécrit en t' selon R si et seulement
il existe une règle l® r de R telle que t se
réécrit, par l® r, en t'. On note
t®*Rt' ou simplement t®*t'
lorsqu'il n'y a pas ambiguïtésur le système de réécriture.
- 1
- La seule exception étant le passage par
référence àune fonction
- 2
- En fait, on àallouédeux pointeurs : un pour le
champs head de la structure DItem et un second pour la
nouvelle liste elle-même.
- 3
- A ne pas confondre avec last
- 4
- Par analogie avec le strcat de C.
- 5
- Parcours préfixe
This document was translated from LATEX by HEVEA.




